设计思想来源于生物学自繁殖的思想，因而它在生物学上的应用更为自然而广泛。例如元胞自动机用于肿瘤细胞的增长机理和过程模拟，人类大脑的机理探索[4]，艾滋病病毒HIV的感染过程[5]，自组织、自繁殖等生命现象的研究。元胞自动机是一个在时间和空间上都离散，通过局部元胞的相互作用而引起全局变化的动力系统。散布在规则格网格中的每一个元胞取有限离散状态，遵循同样的作用规则，依据确定的局部规则作同步更新。大量元胞通过简单的相互作用而构成动态系统的演化。AHMED等[6-7]定义了一类基于元胞自动机的传染病模型，讨论了传播强度的影响及传播结果的分类。 SIRAKOULIS等[8]、FUENTES等[9]利用元胞自动机分别建立了SIS和SIR模型，研究了人群移动、接种疫苗以及人口初始分布等因素对疾病传播的影响。LANGLAIS等[10]通过元胞自动机研究了SEIR传染病模型。谭欣欣等[11]考察了元胞自动机上SEIR模型的种群移动比例和种群移动最大距离对传染病传播的影响。畅春玲等[12]考虑了具有垂直传播的传染病模型。杨婵等[13]研究了异质网络下含有相关系数的SIR传染病模型。但是有一类受季节性影响的传染病却少有人研究，如手足口病、肺结核病等。本文将研究基于二维元胞自动机的一类具有季节性和接种疫苗的SIR传染病模型。
1元胞自动机理论
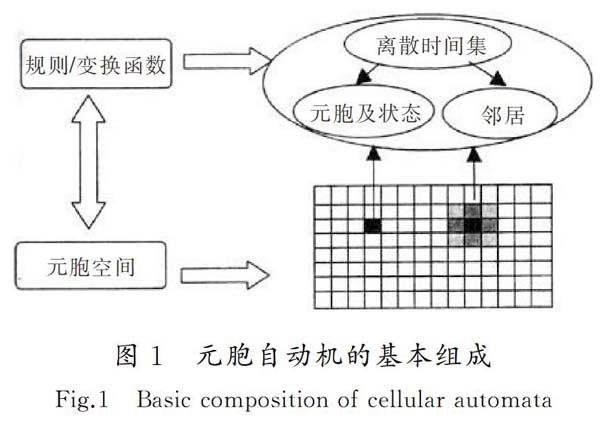
元胞自动机最基本的组成如图1所示，可分为元胞、元胞空间、邻居及演化规则4部分[14]，可用一个四元组表示：CA={Ld，S，N，F}，其中Ld代表元胞空间，d代表空间维数，S为元胞的有限状态集，N表示一个所有邻居内元胞的组合，包括中心元胞在内，是包含n个不同元胞的空间矢量，n为邻居元胞个数，F表示局部转换函数，也就是演化规则。元胞状态的变化依赖于自身的状态和邻居的状态，且某个元胞下一时刻的状态只决定于邻居的状态以及自身的初始状态。
以常用的规则四边形网格划分为例，二维元胞自动机的常用邻居结构可以分为Von Neumann型和Moore型2种。Von Neumann型的元胞邻居数目为2d，Moore型的邻居数目为3d-1，如图3所示。本研究采用半径为1的Moore型邻居结构。关于元胞自动机的具体基本知识可参考文献[15]。
2模型
笔者将人群分为3类：易感者（S）、染病者（I）和恢复者（R），假设疾病的传播是通过染病者和易感者直接接触传染的，在模型中考虑个体出生、自然死亡、因病死亡以及易感者接种疫苗。传染病的传播过程如图4所示。
2.1元胞自动机模型
把这些个体看作是分布在具有J个点的二维环空间上，或者是在一个平面上彼此有联系的J个点。笔者将环和复杂网络或随机网络拓扑映射为一个包含J节点的有限平面L2，这样的结构可以用来描述涉及个体的系统[16]。因此，在这个系统中L2上的每个节点最多被一个个体占据或空着。
笔者用Z（t）={Z1，1（t），Z1，2（t），Z2，1（t），…，Zi，j（t）}，i，j∈N，表示t时刻系统的状态结构，其中Zi，j（t）表示t时刻元胞（i，j）的状态。系统一共有4种状态，分别用-1，0，1，2来表示不同的状态，即Zi，j（t）={-1，0，1，2}，其中-1代表元胞状态为空，0代表元胞状态为易感者，1代表元胞状态为染病者，2代表元胞状态为恢复者。例如，Zi，j（t）=1表示的是t时刻（i，j）的状态为染病者。如果某一元胞在t时刻消亡（自然死亡或因病死亡），则该元胞在t+1时刻状态变为空。在这个系统中，每个元胞都会根据其邻居的状态以一定的概率转变成其他状态，空元胞会以b转化为易感者状态，被占据的元胞会以ε转变为空元胞，染病者会以μ转变为恢复者，或以ε+d转变为空元胞。当然，每个元胞也会保持自身的状态。笔者采用半径为1的Moore型邻居结构，用ni，j（Z，t）表示t时刻元胞（i，j）状态为Z的邻居数量，其中Z∈{-1，0，1，2}元胞的演化规则[17]由表1给出。
2.2平均场近似理论模型
平均场近似理论是研究空间问题应用最广泛和最简单的方法，它认为格子中的每个个体的状态都是独立存在的。HIEBELER[18]研究了元胞自动机上平均场近似的局部扩散和无限扩散，并且模拟了可以用于离散空间模型的一整套方法的2个极端。JIN等[19]研究了基于元胞自动机的平均场近似，同时考虑空间异质易感性的SIR模型。
笔者用x（t）表示t时刻易感者的全局密度，y（t）表示t时刻染病者的全局密度，其中x（t），y（t）∈[0，1]，则有x（t）=N（0，t）J，y（t）=N（1，t）J。用H（t）表示系统的全局密度，则H（t）=N（t）J，H（t）<1，所以有1-H（t）为空元胞的全局密度。其中N（t）为t时刻L2上全部个体的数量，N（t）=∑z=-1，0，1，2N（Z，t），α（t）为有效接触概率，则1-α（t）为没有被传染和保持易感者状态的概率，即易感者不被邻居感染的概率为q=（1-α（t））n（1，t），n（1，t）表示t时刻易感者邻居中为染病者的数目。用δ表示邻居中被占据的数目。因此易感者被邻居传染为染病者的概率为q′=1-q=1-（1-α（t））n（1，t）。在系统中，t+1时刻的易感者数量是t时刻剩余的易感者数量，染病者及恢复者的數量都是如此。由此得到一个非线性离散方程：
x（t+1）=b（1-x（t）-y（t）-z（t））+x（t）（1-K）-px（t）-εx（t），y（t+1）=（1-d-μ-ε）y（t）+x（t）K，z（t+1）=z（t）+px（t）+μy（t）-εz（t），（1）
其中：
K=∑δi=0δiy（t）i（1-y（t））δ-i×
[1-（1-α（t））i]，
表示易感者被邻居感染的概率的期望值，α（t）=β（1+ξ cos πt），其中，β是平均接触率;ξ是接触率的波动幅度，把α（t）代入方程（1）可得到以下模型：
x（t+1）=b（1-x（t）-y（t）-z（t））+x（t）（1-y（t）α（t））δ-px（t）-εx（t），y（t+1）=（1-d-μ-ε）y（t）+x（t）[1-（1-y（t）α（t））δ]，z（t+1）=z（t）+px（t）+μy（t）-εz（t）。（2）
令方程（2）中x（t+1）=x（t）=x，y（t+1）=y（t）=y，z（t+1）=z（t）=z，得到無病平衡点满足的方程：
x=b（1-x-y-z）+x（1-yα（t））δ-px-εx，y=（1-d-μ-ε）y+x[1-（1-yα（t））δ]，z=z+px+μy-εz，（3）
即可得到无病平衡点：
E0=（bε（b+ε）（p+ε），0，pb（b+ε）（p+ε））。
对方程（3）进行泰勒展开，只保留前2项，则有：
x=b（1-x-y-z）+x（1-δyα（t））-px-εx，y=（1-d-μ-ε）y+xδyα（t），z=z+px+μy-εz，（4）
由方程（4）解得：
x*=γδα（t），y*=bεδα（t）-γ（p+ε）（b+ε）δα（t）[b（μ+ε）+εγ]，
z*=pγδεα（t）+μy*ε，其中γ=ε+μ+d，当δ>γ（p+ε）（b+ε）bεα（t）时，模型存在正平衡点E*=（x*，y*，z*）。
3模型的数学分析
为了分析无病平衡点在平均场近似模型中的稳定性，将方程（2）线性化，则有：
x（t+1）=b（1-x（t）-y（t）-z（t））+x（t）（1-δy（t）α（t））-px（t）-εx（t），y（t+1）=（1-d-μ-ε）y（t）+x（t）δy（t）α（t），z（t+1）=z（t）+px（t）+μy（t）-εz（t），（5）
得到无病平衡点E0处的Jacobian矩阵为
JE0=1-b-ε-p-b（1+δεα（t）（p+ε）（b+ε）-b01-γ-bδεα（t）（p+ε）（b+ε）0pμ1-ε。
计算3阶JE0在给定参数值时的谱半径。如表2所示，当δ<4时，ρ（JE0）<1，即此时无病平衡点是局部渐近稳定的;当δ>4时，ρ（JE0）>1， 则无病平衡点是不稳定的。其中b=0.04，ε=0.001，μ=0.12，p=0.004，β=0.2，ξ=0.28。
4数值模拟与结果
笔者利用Python软件对系统进行了数值模拟，设置了不同的初始患者状态，考察其对传染病传播速度的影响。
从图5可以看出，在正平衡点处染病者随着元胞邻居结构δ的增大而增加。图6表示方程（2）在δ=4，ρ（JE0）=0.998 2时的模拟结果。图7至图13显示了传染病在时间和空间都离散的元胞自动机上的模拟。假设在200×200的规则方格中，采取半径为1的Moore型邻居结构，在t=0时，即初始化状态，取1/10的格子令状态为空，100个格子状态为染病者，分为2种情况：1）初始患者在元胞自动机上为中心分布。2）初始患者在元胞自动机上为随机分布。其中β=0.2，ξ=0.28。图7和图8分别为初始患者为中心分布和随机分布时的元胞自动机模拟结果，可以看到初始患者为中心分布的传播速度要小于初始患者为随机分布的传播速度。图9表示不同的2种初始患者状态在元胞自动机上每个时刻易感者、染病者、恢复者的数量变化。图10和图11表示当p=0.006时，不同的初始患者分布的元胞自动机模拟结果，与图7和图8比较，可以看出不同的p值对传染病传播速度的影响，当p值增大时，元胞自动机上疾病的传播速度会变缓。图12和图13反映了不同的p值对初始患者为中心分布的传播速度的影响要大于随机分布的影响。接种疫苗对季节性传染病可以起到一定的减缓作用，这和一般的常微分方程模型的结果一样，所以说用元胞自动机模拟传染病的传播是可行的，可以为研究传染病提供更多的方法。
本研究基于二维元胞自动机，考虑了具有季节性传染和接种疫苗的SIR模型，考察了影响传染病传播速度的原因，影响因素很多，模型有一定的局限性。后期可以研究当染病者分为有症状和无症状的两种情况，对有症状的染病者采取隔离措施，进一步分析传染病的传播情况。
参考文献/References：
[1]BAILEY N T J. The mathematical theory of infectious diseases and its applications[J]. Immmunology， 1977，28（2）：479-480.
[2]ANDERSON R M， MAY R M. Infectious Diseases of Humans： Dynamics and Control[M]. England：Cambridge University Press， 1991.
[3]CHOPARD B. Cellular automata modeling of physical systems[J]. Computational Complexity， 1998：865-892.
[4]VICTOR J D. What can automaton theory tell us about the brain？[J]. Physica D： Nonlinear Phenomena， 1990， 45（1/2/3）：205-207.
[5]SIEBURG H B， MCCUTCHAN J A， CLAY O K， et al. Simulation of HIV infection in artificial immune system[J]. Physica D：Nonlinear Phenomena，1990，45（1/2/3）：208-227.
[6]AHMED E， AGIZA H N， HASSAN S Z. On modeling hepatitis B transmission using cellular automata[J]. Journal of Statistical Physics， 1998， 92（3/4）：707-712.
[7]AHMED E， AGIZA H N. On modeling epidemics including latency， incubation and variable susceptibility[J]. Physica A Statistical Mechanics & Its Applications， 1998， 253（1/2/3/4）：347-352.
[8]SIRAKOULIS G C， KARAFYLLIDIS I， THANAILAKIS A. A cellular automaton model for the effects of population movement and vaccination on epidemic propagation[J]. Ecological Modelling， 2000， 133（3）：209-223.
[9]FUENTES M A， KUPERMAN M N. Cellular automata and epidemiological models with spatial dependence[J]. Physica A Statistical Mechanics & Its Applications， 1999， 267（3/4）：471-486.
[10]LANGLAIS M， SUPPO C. A remark on a generic SEIRS model and application to cat retroviruses and fox rabies[J].Mathematical and Computer Modeling，2000，31（4/5）：117-124.
[11]譚欣欣， 戴钦武， 史鹏燕，等. 基于元胞自动机的个体移动异质性传染病传播模型[J]. 大连理工大学学报， 2013，53（6）：908-914.
TAN Xinxin，DAI Qinwu，SHI Pengyan，et.al.CA-based epidemic propagation model with inhomogeneity and mobility[J]. Journal of Dalian University of Technology， 2013，53（6）：908-914.
[12]畅春玲， 隋英， 孙艳玲. 具有垂直传播和一般接触的元胞自动机传染病模型[J]. 科技广场， 2010（6）：132-134.
CHANG Chunling，SUI Ying，SUN Yanling.Cellular automata model for epidemics with the characteristic of vertical tarnsmission and contact[J].Science Mosaic，2010（6）：132-134.
[13]杨婵，张菊平.异质网络下含有相关系数的SIR传染病模型的建立和分析[J].河北工业科技，2018，35（1）：7-11.
YANG Chan，ZHANG Juping. Establishment and analysis of SIR epidemic model with correlation coefficient under heterogeneous network[J]. Hebei Journal of Industrial Science and Technology， 2018，35（1）：7-11.
[14]陕振沛， 宁宝权， 郭亚丹. 采用元胞自动机的甲型H1N1流感传播模型研究[J]. 六盘水师范学院学报， 2013，25（2）：73-76.
SHAN Zhenpei，NING Baoquan，GUO Yadan.Transmission of influenza a （H1N1） model of cellular automata adopted for research[J].Journal of Liupanshui Normal University，2013，25（2）：73-76.
[15]YACOUBI S E， JAI A E. Cellular automata modelling and spreadability[J]. Mathematical & Computer Modelling， 2002， 36（9）：1059-1074.
[16]LI Ying， LIU Yang， SHAN Xiuming，et al. Dynamic properties of epidemic spreading on finite size complex networks[J]. Chinese Physics， 2005， 14（11）：2153-2157.
[17]LIU Quanxing， JIN Zhen. Cellular automata modelling of SEIRS[J]. Chinese Physics， 2005， 14（7）：1370-1377.
[18]HIEBELER D. Stochastic spatial models： From simulations to mean field and local structure approximations[J]. Journal of Theoretical Biology， 1997， 187（3）：307-319.
[19]JIN Zhen， LIU Quanxing. A cellular automata model of epidemics of a heterogeneous susceptibility[J]. Chinese Physics， 2006， 15（6）：1248-1256.
