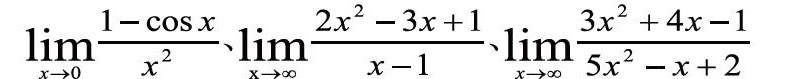体会不到数学带来的乐趣。
（三）教学方法
学生的数学水平参差不齐是事实，教师在教学的过程将精力重点放在科研之上，疏于对新式教学方法的研究，一直沿用传统的教学方式，学生们上课时没有学习的热情。此种情况下，教师一直在不停地讲课，学生们听的人较少，致使教师的辛苦成为无用功，无法达到教学目的。
3 高职数学教学中“教学做合一”教学模式应用建议
（一）切实提高思考能力
对于高职数学教学来说，学生们厌学的重要原因之一就是读不懂题意。数学本身就是认知世界和改造世界的有力工具，教师应该在课堂当中引导学生在学习的时候能够进行独立思考。不然学生无法产生单独思考的能力，离开教师的引导就不知道如何学习，对学生未来的发展不利。能够顺畅地读懂数学知识，要求学生在看到数学知识或题目时，能够快速读懂其表达的意思，而在阅读完成之后能够在头脑中对这段意思有清晰的感受，并能通过自己的语言方式进行描述，这就是形成了属于自己的思考。在思考的同时还要能够立刻联想到与之相关的公式、定理、图像等。比如教师在教导学生学习洛必达法则（一）、（二）之后，学生应该知晓其可以被说成是“函数之比的极限等于其导数之比的极限”，并迅速想起已经学习的几个极限：
251431132cos1222x20limlimlim+..+.+..∞→∞→→xxxxxxxxxxx、、
的相关计算。教师通过适当的引导，让学生们通过阅读把握知识要点，逐渐增强理解能力，不断锻炼阅读能力，提升数学的领悟水平。
教师首先要明确教学目标、能力目标以及情感目标，让学生懂得学习数学的目的，重点需要掌握的数学技能，还有数学知识是由哪些方面推广而来的，如后如何应用在实际问题之中。此外，教师还要讲阅读材料分解成为几个部分，形成清晰的知识梯度，引导学生一步步去研究探索，在必要的时候教师直接实施干预，帮助学生度过难关。在这样的过程中，无论学生是否顺利完成学习任务，学生都会逐渐掌握解决数学问题的方法，达到了让学生动脑思考的目的，逐渐疏导熏陶，思考技能也就逐渐提升。
（二）让学生在解决问题中探索知识
结合教学要求，考虑学生的实际情况，教师应该尽量细致地把数学教学内容逐步分解成为一个个细小的部分，形成一个个问题，每个问题都代表了一个侧重点，难易程度循序渐进，组成一个由易到难的学习阶梯，彼此互相连接在一起环环相扣，最终将数学中的知识重点形成一个知识网络，学生解答问题的过程中也就是学习知识的过程，而且有效地发挥了学生的主动性。
教师每次制作出一道这样的“题”就让学生进行解答，学生的阅读、观察、猜测都属于“做”的范围，每堂课的知识都可以成为几个板块，随意拿出一个板块让学生解答，尽量让全部学生都参与其中。这样就实现了“做”的目的，学生们可以检验自身的不足，教师可以检验自己在教学工作中的缺陷。学生在解答问题板块的时候就会产生疑惑，得不到解决心中就会被激发起探索的斗志，让学生的探索的欲望强烈起来。教师应该在这个过程中不断观察学生们的动态，尽量及时发现问题及时解决。
有些教师在讲解的过程中会面面俱到，这样学生也会理解知识，但这种情况下学生处于被动的局面，教师的推导演讲虽然起到了一定作用，但是一定程度上削弱了学生们知识的掌握能力。可以转换一下观念，教师应该发掘学生的主观能动性，让学生通过自身的努力学习知识、理解知识，然后彼此之间交流心得，彼此互相促进，这种形式可以让学生迅速成长，对知识理论的掌握程度更深刻。
（三）引导学生互相沟通交流
学生们的互相交流沟通是学生们之间的“教”和“学”，数学基础较差的可以在这个过程中达到“学”的目的，而数学基础好的学生则具备“教”的能力，这样用基础好的学生带动基础不好的学生，可以有效提升班级数据教学的整体水平。正是因为学生们的数学水平存在差异，必须之间才能发出磨合的火花，在你来我往中形成默契，增强团队合作意识。这种方式可以让原本在学习中落后的学生重新燃起对数学学习的渴望，原本不敢提问的问题也顺利得到解决。数学水平较高的学生在这个过程中输送出自己的数学感悟，帮助了同学，体现了自身的价值，会获得不小的成就感，这种感觉是愉悦的。
高职数学教师在这个过程中，要以激励的方式鼓舞学生参与到交流之中，在学生出现错误的时候要保持宽容，让学生们感受到公平、平等的氛围，如此学生在学习的过程中身心放松。尽可能将以生动、直观的方式让原本的数学知识变得有趣，比如可以使用故事、或者图像等方式展示数学知识，让学生们易于消化。在学生们通过自身努力获得了新知识、找出新答案的时候，教师不要吝啬自己的夸奖，适度的夸赞是进步的动力。教师还要对那些自己探索出问题新解法的学生进行肯定，将其探索出的新方法分享给学生们，指出其中的好处。比如教师在讲到不定积分换元法的时候，教师给出一套层次分明、难易有序的组合题时，学生们互相讨论应该使用何种方法进行解答。讨论当中，学生们会出现由简单到复杂、由笨拙到巧妙的蜕变，各种不同的变量换元方式纷纷被学生们研究出来。教师在一旁适度地引导，可以让学生们瞬间就对不定积分换元的特性、规律进行了解，学生们获得深刻印象，探索热情和能力得到较大提高。
（四）教师适当指点
实际上，教学本身就是一门艺术，有其精妙所在，教师不需要将所有知识全部讲解一遍，要懂得如何进退取舍，关键在于适当的指点，正好能够戳到学生们的疑难点，让学生们心中有疑惑得到教师指点时瞬间有醍醐灌顶的感觉。教师应该通过指点让学生们掌握符合自身特点的思维方式，让学生拥有脱坡种种难处的利器。例如，教师在讲解“洛必达法则”的时候，应该先引导学生们知道这个法则应该应用在哪些类型的极限之中以及如何使用此法则求取极限。然后拿出套题，让学生们自行讨论，使其通过自己的努力掌握这个法则的基本用法。教师引诱学生回到使用洛必达法则能否求出“∞∞或者00
”的极限，学生会给出肯定回答，教师顺势让学生们研究极限xxxxxeeeexxx..∞→∞→+.+.limlimx1cos和，学生实际求解一下，发现此法则失
效，进而让学生们明白此法则在特殊情况无法发挥作用，且没有导数之比原极限也可存在。同时学生们领悟到如何在求极限的过程中灵活使用各种方法。教师的指点并非直接说出结论，而是让学生参与到结论的探索之中，让学生自己沿着教师给定的方向开展探索，不仅会接触到问题的各个方面，也会让学生逐渐掌握各种方法，逐渐具备解题的智慧。在“做”的同时实现“学”与“教”，让教学与学习充满乐趣，学生在克服困难的同时逐步锻炼各方面的能力，培养了学生的心智，让学生在面对学习困难的时候懂得凭借自身的探索去寻找答案。
总结：高职院校是我国培训人才的重要教育场所，提升学生的技能能够对社会的发展作出贡献。数学与物理、化学、生物等科学领域都存在重要联系，是各类科学工作顺利开展的有力工具。提升学生的学习热情，让学生在掌握数学理论的同时可以将其顺利地应用在现实问题的解决之中，将“教学做合一”的教学模式应用在高职数学教学之中就可以顺利达到这个目的，为国家培养出更多人才，对我国教育事业的健康发展作出重要贡献。
参考文献
[1]梁萌.提高中职数学教学课堂效果的几点思考[J].河南科技.2013（06）：114-115.
[2]庞淑萍，孙莉，张铁军.启发式教学法在经济数学教学中的应用[J].林区教学.2011（05）：214-215.
[3]罗伟.探讨求函数极限的三种常用方法[J].数学学习与研究.2011（01）：148-151.
[4]路百秀，崔锋杰，王民江.教学做合一构建中职专业课教学模式[J].中国现代教育装备.2011（08）：205-207.
[5]俞国.论“教学做合一”思想对高职院校构建实践教学体系的意义[J].扬州教育学院学报.2011（03）：47-49.
[6]沈萍，万旭成.构建“教学做合一”的过程信息评价系统[J].浙江工商职业技术学院学报.2011（03）：224-226.
[7]张晶，徐金寿.论高职教学中的“教学做合一”[J].职业教育研究.2011（03）：107-109.
[8]陈亚楠.“双化”教学中怎样做到教学做合一[J].现代教育.2011（Z2）：209-211.
[9]张海燕，薛明志.实变函数课程教学方法研究与实践[J].赤峰学院学报（自然科学版）.2015（03）：178-179.
[10]徐小明，邱翔，门少平，庞莉莉.“实变函数”课程教学改革探讨[J].中国电力教育.2014（23）：56-58.
[11]蔡懿博.“教学做合一”数学方法在中职数学教学中的运用思路[J].数学学习与研究.2014（11）：325.
[12]莫海平.绥化学院实变函数课程建设改革综述[J].绥化学院学报.2013（09）：146-148.
作者简介
卿雪梅，女，四川省广安市，大学本科，讲师，广安职业技术学院，研究方向：数学与应用数学。
